Star and Gas Formation
Contents
5. Star and Gas Formation¶
5.1. Star Formation in the Local Universe¶
Roughly 25% of local star formation happens in starburst galaxies, which have SFR of a few to \(1000\) \(M_\odot\) per year.
The other 75% of star formation takes place in normal spiral galaxies with \(0\) to a few solar masses per year.
Star formation takes place in giant molecular clouds, with masses of 100,000 to a million solar masses.
These extend over a few tens of parsecs, and are typically cold with \(T \sim 10\) K.
Star formation is an inefficient process, needing \(\sim 10 M_\odot\) of gas for every solar mass formed.
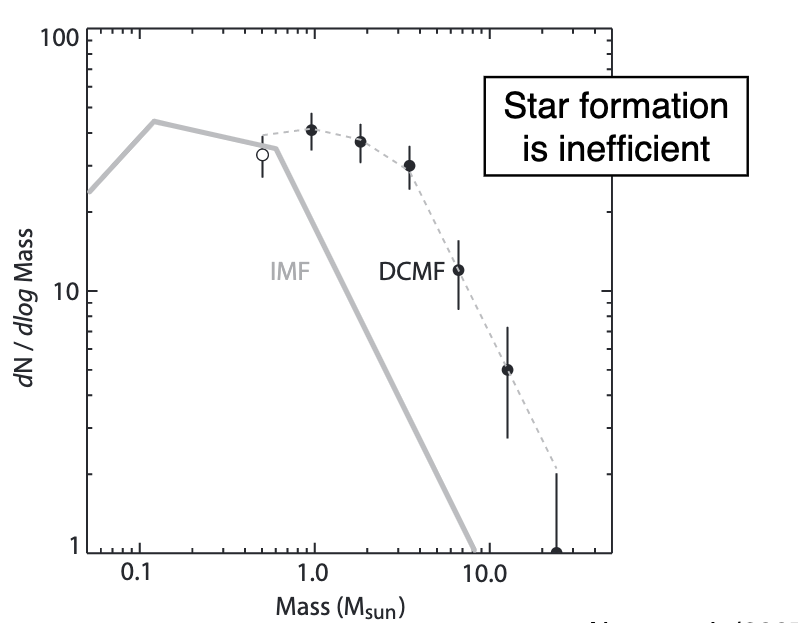
5.1.1. Jeans Mass and Cloud Fragmentation¶
The free-fall timescale is given by \(t\sim (G\rho)^{-1/2}\), whereas the
timescale for pressure is the sound crossing time: \(t \sim R/v_s\).
Gravity wins when the free-fall time scale is shorter than the pressure timescale:
And the Jeans mass is simply the mass contained inside a sphere of the Jeans length.
5.2. Star Formation Rate Indicators¶
Fundamental question: My galaxy has massive stars that I cannot necessarily observe. Can we find indicators for ongoing star formation?
A really excellent page is here.

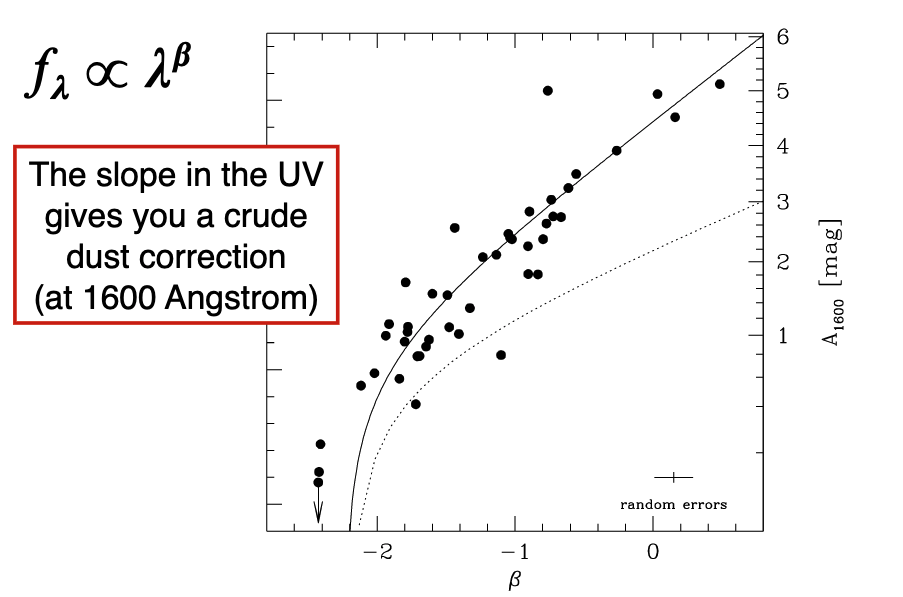
5.2.1. UV Emission¶
UV is really great for massive stars greater than about \(M>3 M_\odot\). These are MS stars with \(T> 10,000\)K or so, and lifetimes of 10-100 Million years.
We can use this emission (corrected for dust with a \(\beta\) slope) to estimate the SFR of a galaxy.
This is because O and B stars set the UV slope, and these are sensitive to recent star formation.
Assumptions:
Correct for \(\beta\) slope
Need to assume an IMF
Then you can use the Kennicutt SFR relations:
SFR \(\propto L_\nu\) where \(\nu\) is over the UV continuum.
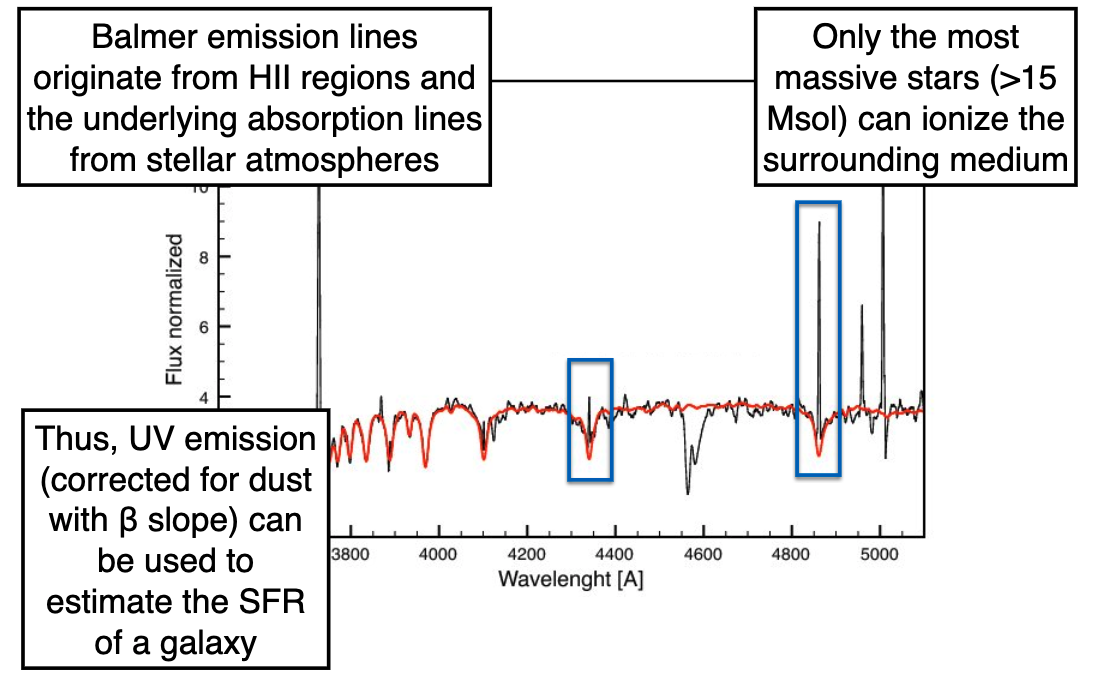
5.2.2. Recombination Lines¶
Balmer emission lines lower \(n=2\) state originate from HII regions and from stellar atmospheres.
Only really massive stars \(M>15M_\odot\) can actually ionize the surrounding medium.
The continuum will be set by the stars, but the emission lines are only from the most massive ones.
We are incredibly sensitive to the IMF choice since we need the most massive stars for H\(\alpha\) for example.
Assumptions:
Assume a metallicty
Assume dust correction
Assume we know the IMF
Binarity
5.2.3. Far IR Emission¶
Far IR emission \((>10 \mu m\) or so) comes mostly from attenuated UV light from massive stars and serves as a SFR indicator.
We need to combine the UV and FIR SFRs and can convert total IR luminosities to SFRs.
5.2.4. X-ray Emission¶
High mass x-ray binaries have a very short lifetime (~20 million years) and their X-ray luminosity can thus serve as SFR indicators
5.2.5. Radio Emission¶
Free-free emission from relativistic electrons dominates spectra near 100 GHz as long as it can be disentangled from cold dust emission.
Hydrogen gets ionized from massive stars and radio recombination lines cascade.
This portion of the spectrum is free of dust effects and thus is a gold standard for SFR indicators. It comes without dust and directly from HII regions.
``This is understandable because massive star-formation activities like supernova explosions, their shocks, and remnants increase the number density of high-energy cosmic-ray electrons (CREs) and/or accelerate them, on one hand, and amplify the turbulent magnetic field strength, on the other hand. The net effect of these processes is a strong nonthermal emission in or around star-forming regions.’’
5.3. Molecular Gas in Galaxies¶
5.3.1. The Kennicutt-Schmidt Law¶
Another way to trace star formation is to trace the amount of gas available in galaxies.
Star formation happens in H2 clouds, but these are notoriously hard to observe.
We want to measure \(\Sigma_{gas} = \Sigma_{H2} + \Sigma_{HI}\) but typically have to measure \(\Sigma_{gas} = \Sigma_{HI} + \alpha_{CO}I_{CO}\) to approximate the H2 content.
HI is extremely easy to measure from the 21 cm line.
\(\alpha\) is calibrated locally and extrapolated outward
Note that \(\alpha\) is metallicity dependent.
Even more common is to measure dust content and convert dust to CO content since dust is really easily observable.
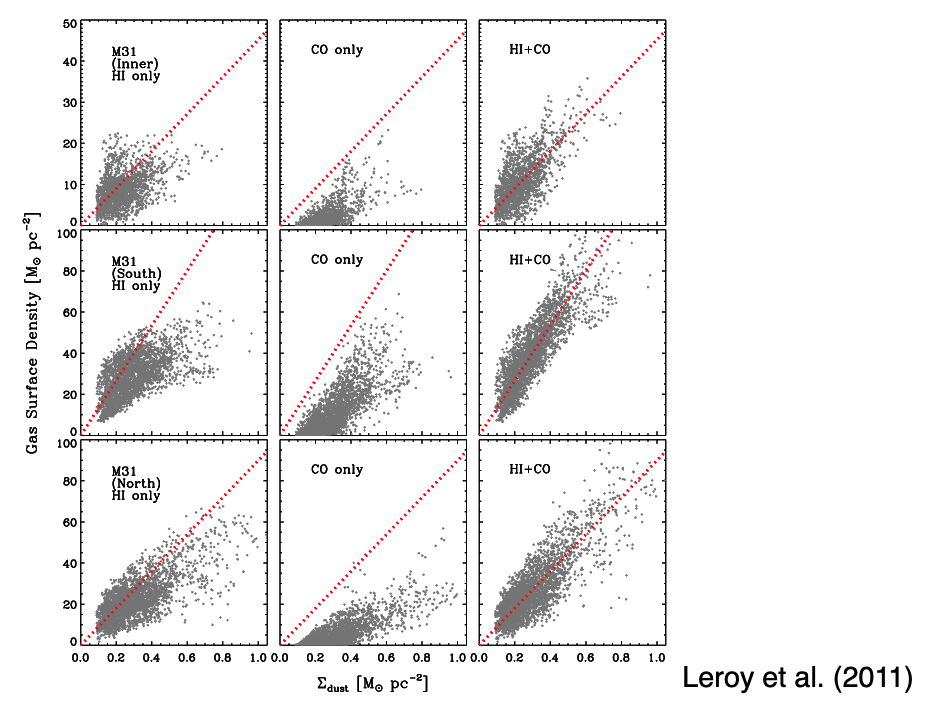
The reason we care about measuring gas is because of the Kennicutt-Schmidt Law:
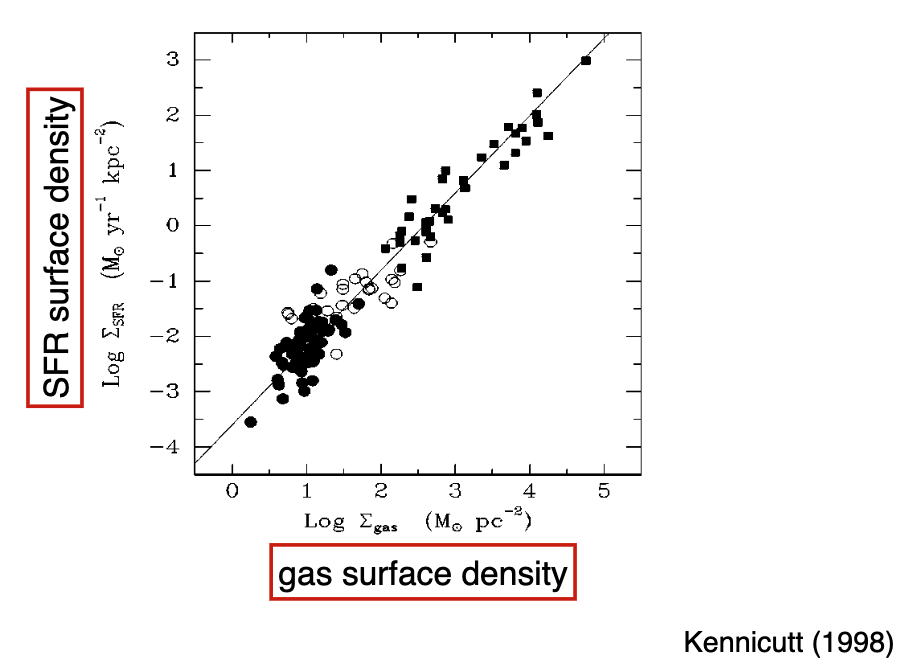
5.3.2. Summary¶
Stars form in dense molecular clouds of molecular hydrogen (HI doesn’t get dense enough).
Star formation rates can be measured from different indicators, each with pros and cons.
The CO-H\(_2\) conversion depends on the metallicity since, at lower metallicity, CO can be photodissociated.
The star formation rate surface density scales with molecular gas surface density.
The star formation efficiency is thought to be set by turbulence driven feedback in GMCs.
