7. Dark Matter¶

7.1. Dark Matter Power Spectrum¶

Let $\delta(\mathbf x)$ represent the matter overdensity, a dimensionless quantity defined as:

\[ \delta(\mathbf x) = \frac{\rho(\mathbf x) - \bar\rho}{\bar\rho}, \]

where $\bar\rho$ is the average matter density over all space.

The power spectrum is most commonly understood as the Fourier transform of the two-point correlation function, $\xi$, mathematically defined as:

\[ \xi(r) = \langle \delta(\mathbf x) \delta(\mathbf x') \rangle = \frac{1}{V}\int d^3 \mathbf x \, \delta(\mathbf x) \delta(\mathbf x - \mathbf r), \]

for $\mathbf r = \mathbf x - \mathbf x'$.

This then determines the easily derived relationship to the power spectrum, $P(\mathbf k)$$, that is $\xi(r) = \int \frac{d^3 k}{(2\pi)^3} P(k) e^{i \mathbf k\cdot (\mathbf x - \mathbf x’)}.$

Equivalently, letting $\tilde \delta(\mathbf k)$ denote the Fourier transform of the overdensity $\delta(\mathbf x)$, the power spectrum is given by the following average over Fourier space:

\[ \langle \tilde{\delta}(\mathbf{k}) \tilde{\delta}^*(\mathbf{k}') \rangle = (2 \pi)^3 P(k) \delta^{3}(\mathbf{k} - \mathbf{k}') \]

(note that $\delta^3$ is not an overdensity but the Dirac delta).

Since $P(k)$ has dimensions of (length)$^3$, the power spectrum is also sometimes given in terms of the dimensionless function:

\[ \Delta^2(k) = \frac{k^3 P(k)}{2\pi^2} \]

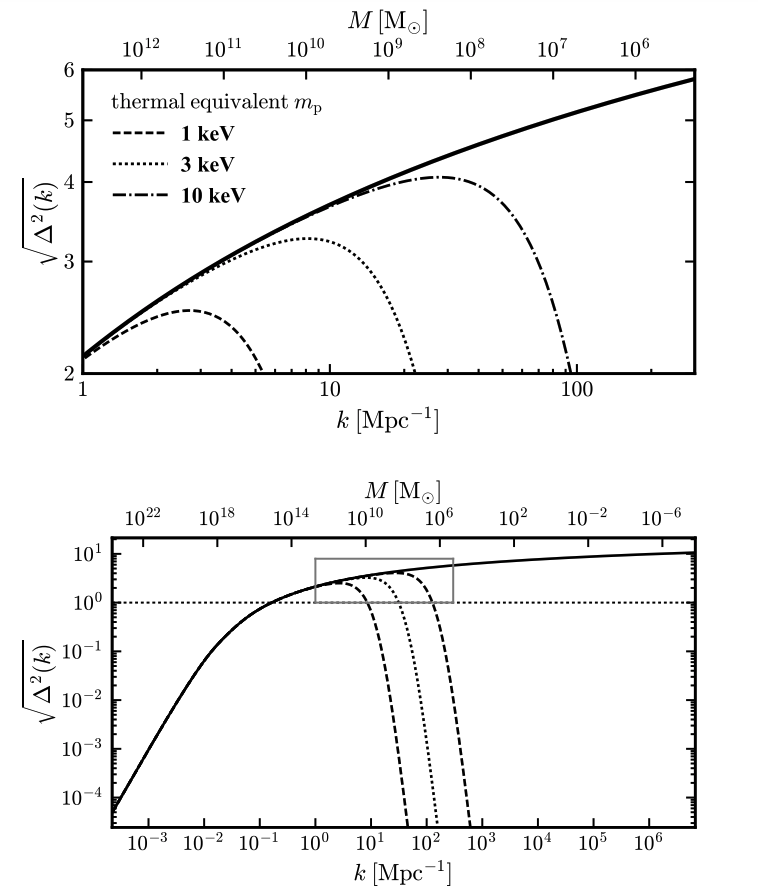
The CDM power spectrum is shown below. We basically have a characteristic distance scale on the $x$ axis and a power on the $y$ axis. Warm dark matter has a turnover in the power spectrum, and thus you lose small scale structure. This is not observed.

7.2. Probes¶

There are a variety of ways we can probe dark matter haloes.
- Rotation curves (from HI for example, which extends to very very large radii beyond the extent of the galaxy where you are gravitationally dominated by DM).
- X-ray emission from hot gas
- Kinematics of satellites or galaxy clusters
- Gravitational lesning; strong and weak
- Sunyaev-Zeldovich effect

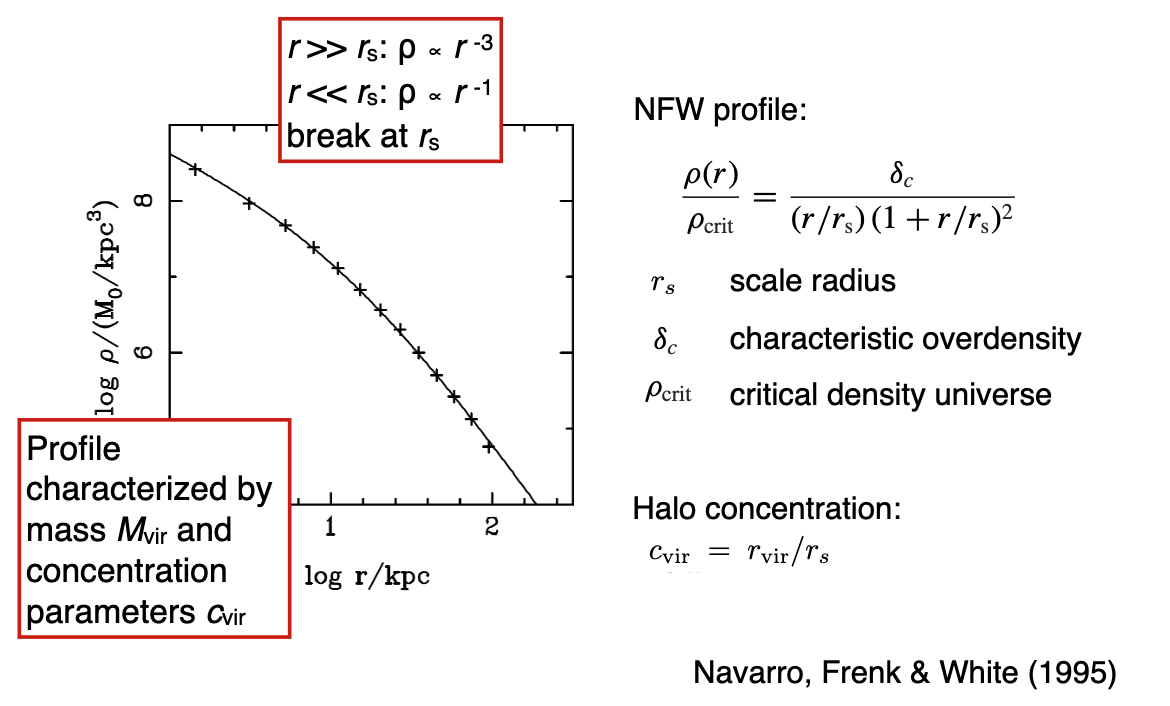
7.3. Dark Matter Halos and the NFW Profile¶

Slightly prolate in shape
Follows approximately NFW profiles:

7.4. Mergers and Halo Growth¶

Halos which formed earlier are more concentrated – dense halos formed early.
Most massive halos today form/assembled later than low mass halos.
Minor mergers are much more common than major mergers.
- More merger products are low mass halos.
Number of mergers per halo per redshift bin barely evolves with time – *
Number of mergers per halo per Gyr was much higher in the past
- Mergers were more frequent in the past!

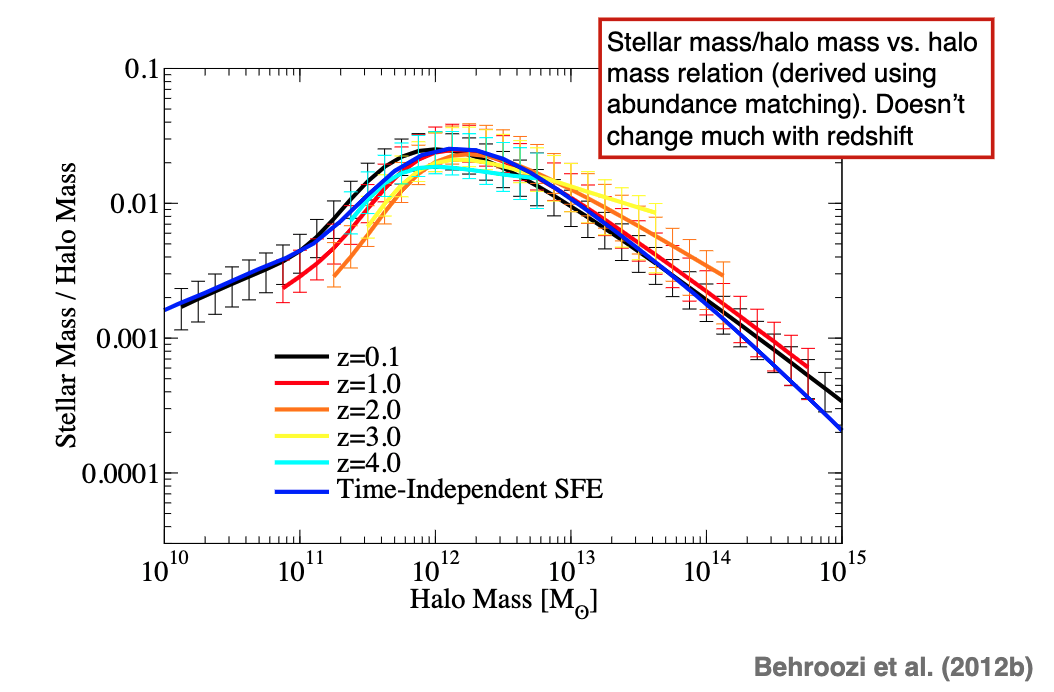
7.5. Stellar Mass-Halo Mass Relation¶

The stellar-mass halo-mass relation really doesn’t seem to depend on redshift. (from abundance matching)

7.6. Problems with “Standard” Cold Dark Matter¶

Missing satellite problem
Cusp-core problem
Halos are triaxial, why don’t we see that?
Why are there so many pure disk galaxies?
Too few galaxies in voids?

7.6.1. Missing Satellites Problem¶

Standard $\Lambda$CDM simulations show many small satellites around galaxies which we don’t have evidence for.

Potential solutions:
- Low mass halos may not be able to attract/retain their baryonic matter?
- Maybe they were tidally stripped or merged?

7.6.2. Cusp-Core Problem¶

CDM predicts cuspy dark matter density distributions (dashed lines) but we observe central constant density regions
Solution: Baryonic effects (primarily supernova feedback) can alter the density profile of low-mass dark matter halos

7.7. Summary of DM Halo Evolution¶

DMHs that collapse first are more concentrated
More massive DMHs assemble later
The concentration in more massive halos evovle slower as more late-time mergers lead to lower concentration parameters
The dark matter halo merger rate can be described with a universal function
- The normalized merger rate per redshift interval is primarily a function of the merger ratio
CDM still has some problems but none are problematic enough to change our paradigm

Stellar Populations & Galaxies

Dark Matter

Contents