.md .pdf

repository open issue

Contents

Turbulence

Disordered flow with a wide range of interacting scales. Vorticity, irregularly distributed in 3D. There’s typically large dissipation of energy, with lots of effective mixing and transportation of pretty much everything that can be transported.

Kolmogorov Spectrum

This describes homogeneous and istropic turbulence.

We really want to solve for the turbulent velocity field:

\[ \vec v (\vec x) = \langle \vec v \rangle + \underbrace{\delta \vec v (\vec x)}_\text{fluctuating part} \]

We go into Fourier space:

\[ \delta \vec v( \vec x) = \int d^3k \, e^{i \vec k\cdot \vec x} \delta \vec v(\vec k) \]

The mean kinetic energy of a turbulent flow per unit mass:

\[ E = \frac12 \int \frac{d^3 \, x}{V} |\delta \vec v( \vec x)|^2 \equiv \int_0^\infty dk \,\underbrace{E(k)}_\text{spectral energy} \]

Dimensionally, we know that:

\[ E(k) \sim \frac{v^2}{k} \sim \frac{\ell^3}{t^2} \]

Now Kolmogorov steps in with some more dimensional analysis (Kolmogorov theory):

An observational fact: energy transfer goes from large scales to small scales.

At high \(\mathcal{Re}\), statistics of isotropic tubulent flow are fully determined by the “energy dissipation rate/cascading rate” (per unit mass): \(\mathcal{E} \sim \frac{\ell^2}{t^3}\). That is to say:

\[ E(k) \propto \mathcal{E}^\alpha k^\beta \sim \frac{\ell^{2\alpha-\beta}}{t^{3\alpha}} \sim \frac{\ell^3}{t^2} \rightarrow \alpha = 2/3, \beta = -5/3 \]

And thus:

\[ \boxed{E(k) \sim \mathcal{E}^{2/3} k^{-5/3}} \]

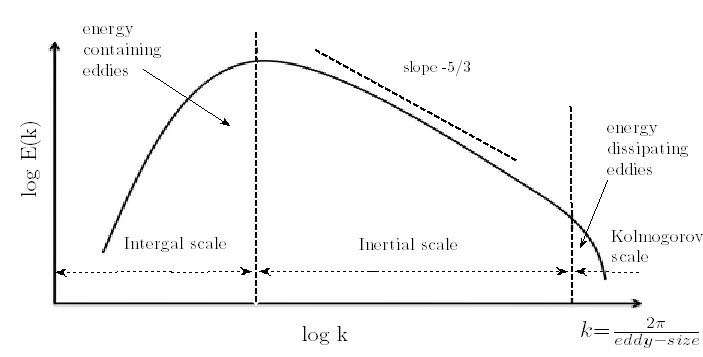
This is the Kolmogorov spectrum, and is a prediction for turbulence. This is only true over some wavelength range defined by \(l_{min}\) and \(l_{max}\). We call \(l_{min}\) the Kolmogorov microscale. Below this scale, viscosity \(\nu\) matters. We find:

\[ l_{min} \sim \left(\frac{\nu^3}{\mathcal{E}}\right)^{1/4} \]

The other end – \(l_{max}\) is determined by the eddy size. We have the “turnaround speed/timescale” of eddy of size \(\ell\). We can show that:

\[ v \sim \left(\mathcal{E} l_{max}\right)^{1/3} \]

where \(v\) is the eddy speed. In the image below, high \(k\) has viscosity that matters. At these scales, the turbulent energy is converted into heat.

And that’s it!

previous

Magnetohydrodynamics