Fitting a Line to Data
Contents
Fitting a Line to Data¶
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.size'] = 16
mpl.rcParams['legend.fontsize'] = 14
mpl.rcParams['figure.dpi'] = 150
Linear Least Squares with Matrices¶
Let’s fit a line of the form:
\[
y = \beta_0 x + \beta_1
\]
Assuming that both y and x are vectors with \(n\) elements, we can rewrite this equation in matrix form:
\[\begin{split}
\begin{bmatrix}
Y_1 \\
Y_2 \\
\vdots \\
Y_n
\end{bmatrix} = \begin{bmatrix}
\beta_0 + \beta_1 X_1 \\
\beta_0 + \beta_1 X_2 \\
\vdots \\
\beta_0 + \beta_1 X_n
\end{bmatrix}
\end{split}\]
\[\begin{split}
\underbrace{\begin{bmatrix}
Y_1 \\
Y_2 \\
\vdots \\
Y_n
\end{bmatrix}}_{Y_{n\times1}} = \underbrace{\begin{bmatrix}
1 & X_1 \\
1 & X_2 \\
\vdots & \vdots \\
1 & X_n
\end{bmatrix}}_{X_{n\times2}} \underbrace{\begin{bmatrix}
\beta_0 \\
\beta_1
\end{bmatrix}}_{\beta_{2\times1}}
\end{split}\]
\[
Y = X \beta
\]
Here, I’ll simulate some data with \(n=25\):
# generate some random, linear data with random error
n = 25
x = np.random.uniform(size=n)
y = 2.4*x + 0.3 + np.random.normal(0,0.1,size=n)
# plot the data
plt.figure()
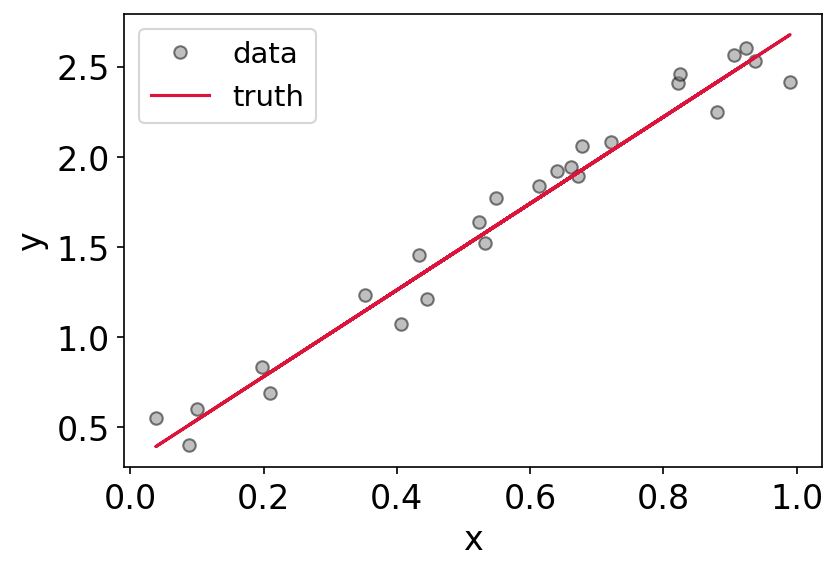
plt.plot(x,y,'o',label = 'data',mfc='gray',markeredgecolor='k',alpha=0.5)
plt.plot(x,2.4*x + 0.3,label = 'truth',color='crimson')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
<matplotlib.legend.Legend at 0x7fe37733f490>
We can now directly solve for the vector \(\beta\) after reshaping our data to the matrix shapes above:
\[
\hat{\beta}=\left(X^{T} X\right)^{-1} X^{T} Y
\]
# first reshape to make these the proper matrix forms
Y = y.reshape((-1,1)) # 100 x 1
# add a vector of ones as a column to X (see above equation)
vector_of_ones = np.ones(n)
X = np.column_stack((vector_of_ones, x))
print('X shape: ', X.shape)
print('Y shape: ', Y.shape)
X shape: (25, 2)
Y shape: (25, 1)
beta_hat = np.linalg.inv(X.T @ X) @ X.T @ Y
print('Beta Shape: ', beta_hat.shape)
Beta Shape: (2, 1)
beta_hat
array([[0.32544314],
[2.38931179]])
# generate a best fit line
x_fit = np.linspace(0,1,10)
y_fit = beta_hat[1]*x + beta_hat[0]
# plot the data, best fit line, and ground truth
plt.figure()
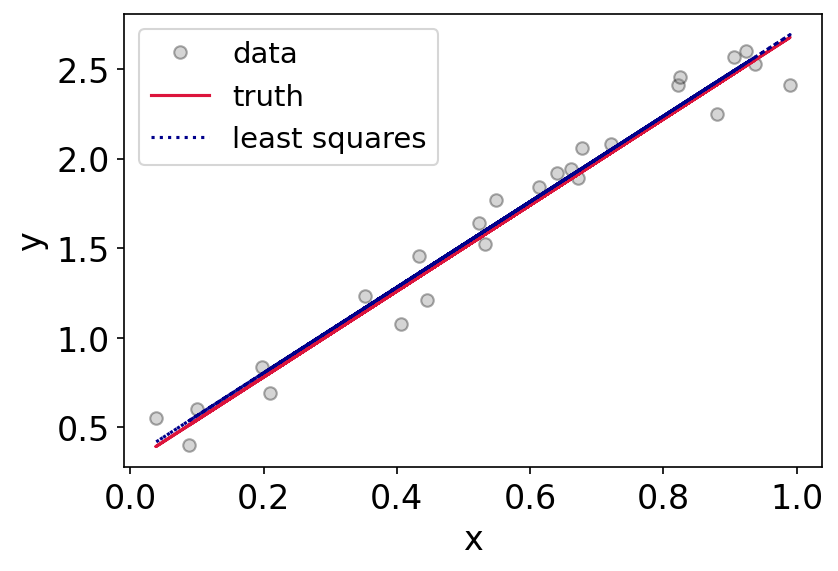
plt.plot(x,y,'o',label = 'data',mfc='gray',markeredgecolor='k',alpha=0.33)
plt.plot(x,2.4*x + 0.3,label = 'truth',c='crimson')
plt.plot(x,y_fit,label='least squares',c='darkblue',ls='dotted')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
<matplotlib.legend.Legend at 0x7fe377a4c810>
Weighted Least Squares¶
What if our data have measurement errors which are not constant? How do we weight our points properly?
We can slightly modify our expression for \(\beta\) above in the case of known measurement errors. For more math, see Section 2.2 of: https://www.stat.cmu.edu/~cshalizi/mreg/15/lectures/24/lecture-24–25.pdf.
Another great resource: https://adrian.pw/blog/fitting-a-line/
The result is that we can define a weight matrix \(W = diag(1/\sigma_i)\) where \(\sigma_i\) are the measurement errors for the \(i\)th measurement. In this case, we have:
\[
{\displaystyle {\hat {\boldsymbol {\beta }}}=(X^{\textsf {T}}WX)^{-1}X^{\textsf {T}}W\mathbf {y} .}
\]
# generate some random, linear data with random error
n = 25
x = np.random.uniform(size=n)
# evaluate the true model at the given x values
y = 1.17*x + 0.1
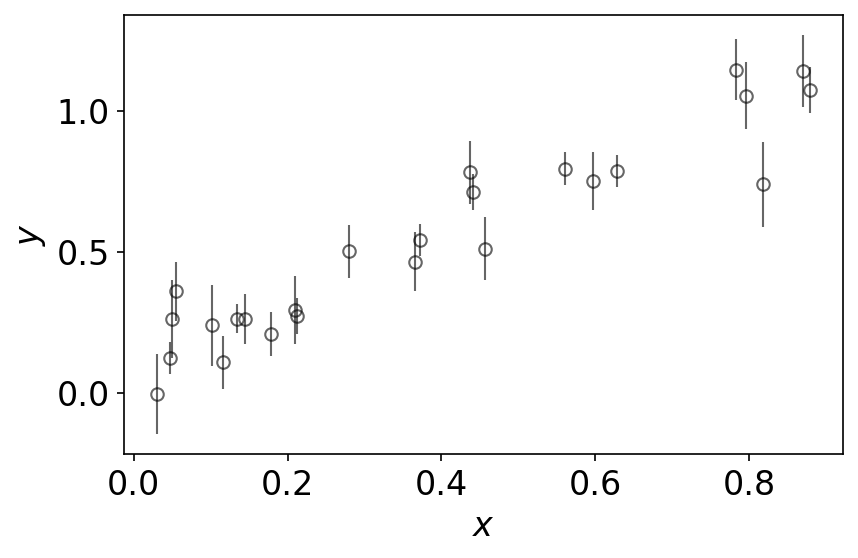
# Heteroscedastic Gaussian uncertainties only in y direction
y_err = np.random.uniform(0.05, 0.15, size=n) # randomly generate uncertainty for each datum
y = np.random.normal(y, y_err) # re-sample y data with noise
datastyle = dict(mec='k', linestyle='none',ecolor='k', marker='o', mfc='none', label='data',alpha=0.6,elinewidth=1)
plt.figure()
plt.errorbar(x, y, y_err, **datastyle)
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.tight_layout()
# solve for beta after defining our matrices
# data matrix
Y = y.reshape((-1,1)) # 50 x 1
# design matrix
vector_of_ones = np.ones(n)
X = np.column_stack((vector_of_ones, x))
# weight matrix
W = np.diag(1/y_err**2)
# solve for beta
beta_hat_weighted = np.linalg.inv(X.T @ W @ X) @ X.T @ W @ Y
beta_hat_unweighted = np.linalg.inv(X.T @ X) @ X.T @ Y
print(f'Weighted Least Squares:\t y = {np.round(float(beta_hat_weighted[1]),4)}x+{np.round(float(beta_hat_weighted[0]),4)}')
print(f'Unweighted Least Squares: y = {np.round(float(beta_hat_unweighted[1]),4)}x+{np.round(float(beta_hat_unweighted[0]),4)}')
Weighted Least Squares: y = 1.175x+0.0903
Unweighted Least Squares: y = 1.1302x+0.103
# generate a best fit line
x_fit = np.linspace(0,1,10)
y_fit_weighted = beta_hat_weighted[1]*x_fit + beta_hat_weighted[0]
y_fit_unweighted = beta_hat_unweighted[1]*x_fit + beta_hat_unweighted[0]
cmap = plt.get_cmap('jet')
dictstlye = dict(mec='k', linestyle='none',ecolor='k', marker='o', mfc='none', label='data',alpha=0.6,elinewidth=1)
plt.figure()
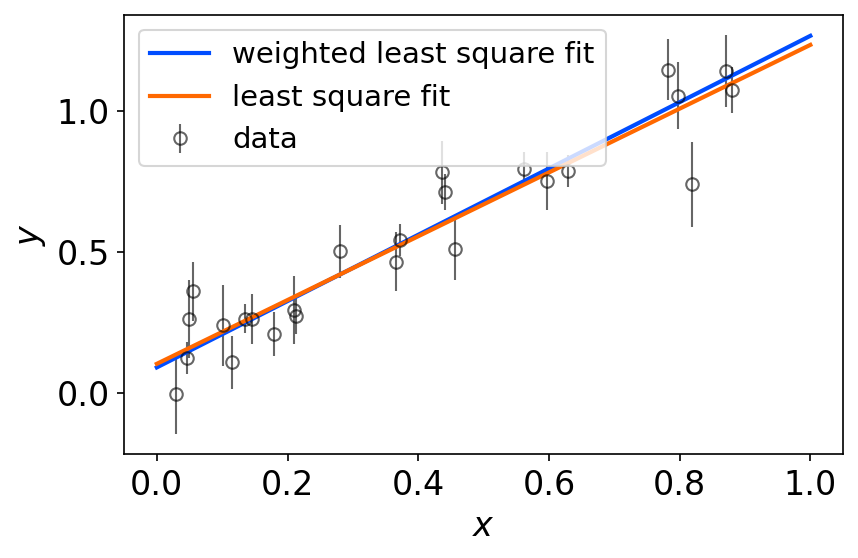
plt.errorbar(x, y, y_err, **dictstlye)
plt.plot(x_fit,y_fit_weighted,color=cmap(0.2/1),label='weighted least square fit',lw=2)
plt.plot(x_fit,y_fit_unweighted,color=cmap(0.8/1),label='least square fit',lw=2)
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.legend(loc='upper left')
plt.tight_layout()
