.md .pdf

repository open issue

Contents

Hydrostatic Equilibrium: A Deep Dive

Force Balance

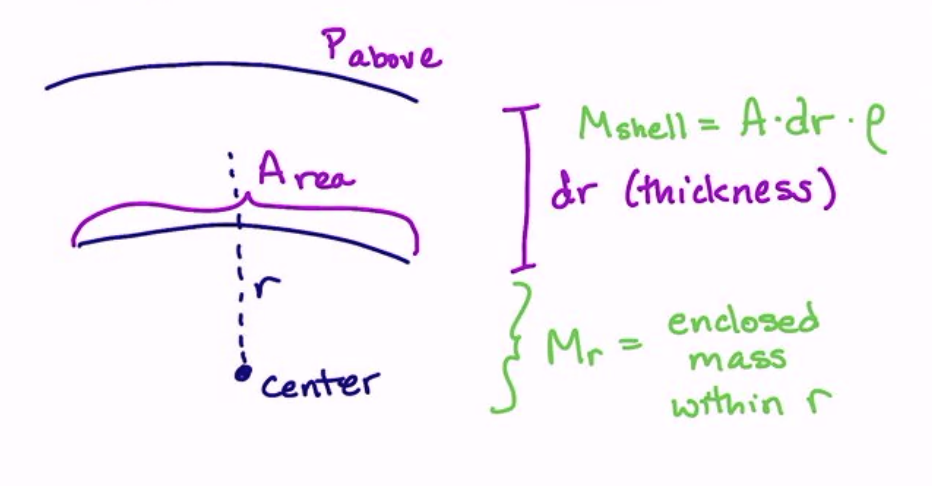
Let us consider a little patch of the surface of the star as a section of a shell. We have an above and below pressure, and an area + thinkness of the patch $dA$ and $dr$. In this thickness, we have some mass $M_{shell} = A \cdot dr \cdot \rho$, and we have the enclosed mass within the shell at radius $r$.

$$P_{above} = P_{below} + dP$$

We then have our force equation:

$$F_{net} = M_{shell} \vec{a} \rightarrow P_{below} \cdot A - P_{above} \cdot A - \frac{G M_r M_{shell}}{r^2} = M_{shell}\vec{a}$$

We can substitute in the pressure equation, giving:

$$-\mathrm{d}P \cdot A - \frac{G M_r \cdot A \rho \mathrm{d}r}{r^2} = A \rho \mathrm{d}r \cdot \vec{a}$$

Simplifying, we have:

$$\boxed{-\frac{\mathrm{d}P}{\mathrm{d}r} - \frac{-G M_r \rho}{r^2} = \rho \vec{a}}$$

Or, sometimes, we see:

$$\boxed{\rho \vec{a} = -\vec{\nabla} P + \rho}$$

We will use hydrostatic equilibrium so often, that we will abbreviate it as $\langle HE \rangle$, and this means that $\vec{a} = 0$.

Doing this, we get, at every radius:

$$\boxed{\frac{dP}{dr} = -\frac{GM_r \rho}{r^2}}$$

And also recall our continuity of mass equation:

$$\frac{\partial M}{\partial r} = 4\pi r^2 \rho(r)$$

An Application of Hydrostatic Equilibrium: Plane Parallel Atmosphere (Isothermal)

Here is the setup of our example: we have something with a surface, gravity, an atmosphere, and a negligible atmospheric mass.

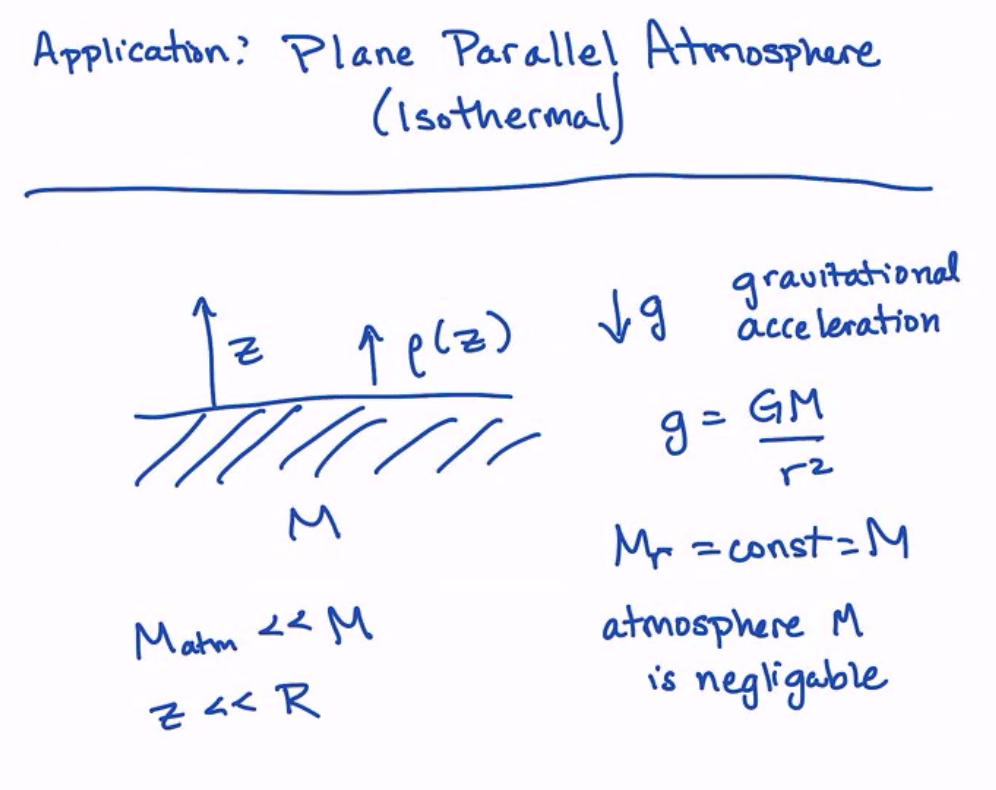
Let’s start with writing the equation of hydrostatic equilibrium for this system $\langle HE \rangle$. We start with:

$$\frac{dP}{dr} = -\frac{GM_r \rho}{r^2}$$

We immediately convert from $r$ to $z$ on the left. On the rightside, we have gravity, which we have defined as $g \equiv -GM/r^2$.

$$\frac{dP}{dz} = - \rho g = -\frac{mP}{kT} g$$

where we have assumed that we have an ideal gas: $P = nkT$. If we also assume that the atmosphere is a single atom or molecule, we have:

$$\rho = n \cdot m$$

If we have a multi-component atmosphere, $m$ is the mean mass per particle. If we make both of these assumptions, we have:

$$\frac{d}{dz} nkT = - nmg \rightarrow \boxed{\frac{dn}{dz} =-\frac{nmg}{kT}}$$

Solving this, we get:

$$\boxed{n(z) = n_0 e^{-z/h} \text{, where } h \equiv \frac{kT}{mg}}$$

and we call $h$ the scale height of the atmosphere and $n_0$ is thje density at $z=0$.

The Solar Surface

The scale height of the sun is $h \sim 2 \times 10^{7}$ cm and the temperature is $T\sim 5800$ K. At the surface, the atmosphere is so thin that properties behave strangely and rapidly with radius. This is because the surface is the boundary from optically thick to optically thin. Thus at the surface, we go from very gradual pressure, temperature, and density changes (with radius) to rapid changes with radius.

Mixed Gas Case

One of the assumptions above is that we have a single type of atom. If we have a mixed gas, we define the mean molecular weight per particle.

For a fully ionized gas, we have the pressure contribution from the ions:

$$P_{ions} = \sum_{i}^{} n_i k T_i$$

where

$$n_i \equiv \frac{x_i \rho}{A_i m_p}$$

where

• $A_i$ is the atomic mass number (for example helium is A=4)

• $x_i$ is the mass fraction

• $m_p$ is the proton mass

We can also impose charge neutrality, and we have:

$$n_e = \sum_i Z_i n_i$$

where

• $Z_i$ is the number of protons per electron in an atom

In this mixed gas, we need the total pressure:

$$P_{total} = P_{ion} + P_{electrons}$$

$$P_{ion} = \frac{kT \rho}{m_p} \sum_i \frac{x_i}{A_i} \equiv \frac{k T \rho}{\mu_I m_p}$$

where

$$\mu_I = \sum \frac{x_i}{A_i}$$

is the mean molecular weight in ions. We also have the electron pressure:

$$P_{electrons} = n_e kT = kT \sum_i Z_i n_i$$

$$P_{electrons} = kT \sum_i \frac{Z_i x_i \rho}{A_i m_p}$$

$$P_{electrons} = \frac{kT \rho}{m_p} \sum_i \frac{Z_i x_i}{A_i}$$

$$P_{electrons} = \frac{\rho kT}{\mu_e m_p}$$

where

$$\frac{1}{ \mu_e} \equiv \sum_i \frac{Z_i x_i}{A_i}$$

All of this gives:

$$\boxed{P_{tot} = P_{ions} + P_{elect} = \frac{\rho kT}{\mu m_p}}$$

where

$$\boxed{ \frac{1}{\mu} = \frac{1}{\mu_I} + \frac{1}{m_{e}}}$$

For a fully ionized plasma,

$$\frac{1}{\mu} = \sum_i \frac{x_i(1+Z_i)}{A_i}$$

For ionized hydrogen, $\mu = 1/2$, but for hydrogen and helium in cosmic abundance, we have $\mu = 0.62$. This changes the structure and radii big time of our stars around us! Microphysics has a huge macro-impact.

previous

Broad Overview of the Class

next

Virial Theorem